Операции над множествами
Обозначение множеств и их элементов. Равенство множеств.
Подмножество ( включение ). Сумма ( объединение ) множеств.
Произведение ( пересечение ) множеств. Разность ( дополнение )
множеств. Симметричная разность множеств. Свойства
операций над множествами.
Множества обозначаются заглавными латинскими буквами, а их элементы –
строчными.
Два множества А и В называются равными ( А = В ), если они состоят из одних и
тех же элементов, то есть каждый элемент множества А является элементом
множества В и наоборот, каждый элемент множества В является элементом множества
А .
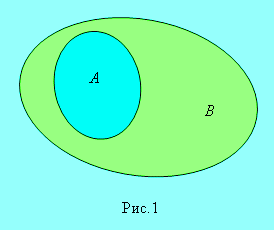
Говорят, что множество А содержится в множестве В ( рис.1 ) или множество А
является подмножеством множества В, если каждый
элемент множества А одновременно является элементом множества В.
Сумма ( объединение ) множеств А и В есть множество элементов,
каждый из которых принадлежит либо А , либо В.
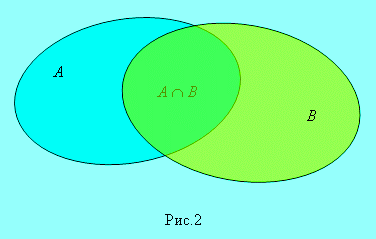
Произведение ( пересечение ) множеств А и В ( рис.2 ) есть
множество элементов, каждый из которых принадлежит и А , и В.
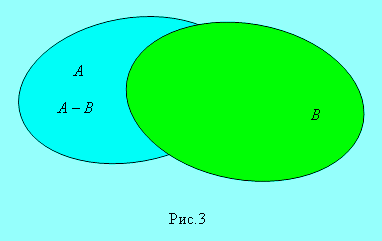
Разность множеств А и В ( рис.3 ) есть множество элементов,
которые принадлежат множеству А , но не принадлежат множеству В. Это множество
называется также дополнением множества В относительно множества А.
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ( В – А ).
Свойства операций над множествами:

П р и м е р ы.
1. Множество детей является подмножеством всего населения.
2. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.
3. Объединением множества рациональных чисел с множеством иррациональных чисел является множество действительных чисел.
4. Нуль является дополнением множества натуральных чисел
относительно множества неотрицательных целых чисел.